Abstract—시공간 정보는 3D 포즈 추정에서 폐색 및 깊이 모호성을 해결하는 데 중요합니다. 이전의 방법은 고정 길이의 시공간 정보를 포함하는 시간적 컨텍스트 또는 로컬에서 전역적 아키텍처에 초점을 맞췄습니다. 현재까지, 다양한 시공간 시퀀스를 동시에 유연하게 캡처하고 실시간 3D 포즈 추정을 효과적으로 달성하기 위한 효과적인 제안은 없었습니다. 본 연구에서는 주의 메커니즘을 통해 국소 및 전역 공간 정보를 모델링하여 인간 골격의 운동학적 제약 조건, 즉 자세, 국소 운동학적 연결 및 대칭에 대한 학습을 개선합니다. 단일 및 다중 프레임 추정에 적응하기 위해 확장 시간 모델을 사용하여 다양한 골격 시퀀스를 처리합니다. 또한, 중요한 것은, 우리는 시너지 효과를 달성하기 위해 시간적 의존성을 가진 공간 의미론적 인터리빙을 신중하게 설계한다는 것입니다. 이를 위해, 우리는 인터리빙된 시간적 컨볼루션과 그래프 주의 블록으로 구성된 단순하면서도 효과적인 그래프 주의 시공간 컨볼루션 네트워크(GAST-Net)를 제안한다. 두 가지 까다로운 벤치마크 데이터 세트(Human3.6m 및 HumanEva-I) 및 YouTube 비디오에 대한 실험은 우리의 접근 방식이 깊이 모호성과 자가 폐색을 효과적으로 완화하고 상반신 추정을 일반화하며 2D에서 3D 비디오 포즈 추정에 대한 경쟁력 있는 성능을 달성한다는 것을 보여줍니다. 코드, 비디오 및 보조 정보는 http://www.juanrojas.net/gast/ 에서 확인할 수 있습니다.
Index Terms— 2D-to-3D human pose, video pose estimation, graph attention, spatio-temporal networks
I. INTRODUCTION
비디오에서 3D 휴먼 포즈 추정은 활동 인식, 가상 현실 및 휴먼 로봇 상호 작용과 같은 영역에 영향을 미치는 매우 활발한 연구 영역입니다. 이전에는 실내 환경에서 깊이 센서, 모션 캡처 또는 멀티 뷰 영상을 사용하여 3D 포즈 추정을 계산했습니다. 그러나 최근 딥 러닝을 통한 2D 인간 포즈 추정의 발전과 함께 야생 데이터의 대규모 가용성으로 인해 단안 이미지에서 3D 포즈 추정을 해결하는 데 큰 진전이 있었습니다 [1]. 최근 작품[2]–[4]은 2D 휴먼 포즈 표현만 사용하고 경쟁적 성능과 일반화를 달성하여 배경 소음과 인간 외관의 영향을 받지 않습니다. 또한 RGB 이미지 처리와 비교할 때, 2D 대 3D 방법은 2D 키포인트(연산을 덜 사용하는)를 활용하고 장기적인 프레임 추정을 가능하게 합니다. 본 논문에서는 2D 대 3D 추정에 초점을 맞춥니다.
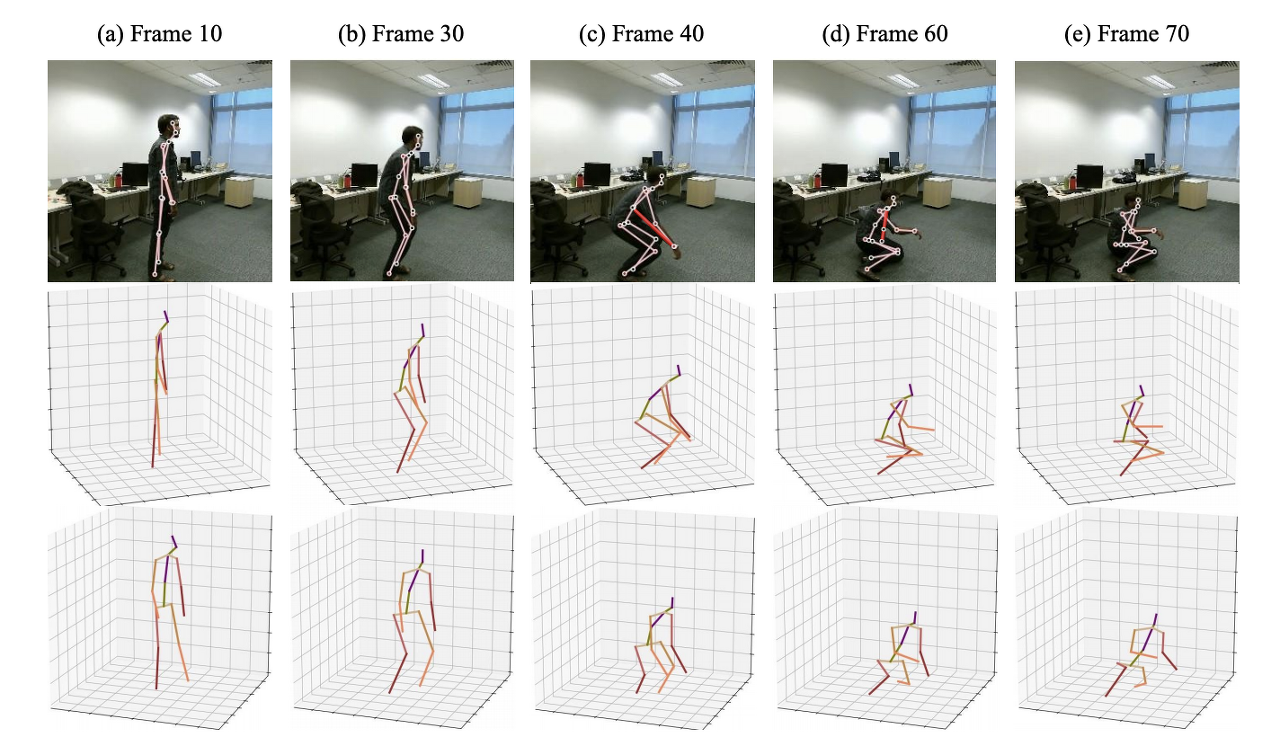
- Fig. 1: Pose estimation reconstruction under depth ambiguities, self-occlusion, and biased 2D poses. Row 1: 2D pose estimation, where red is the prediction with errors. Row 2, 3: our reconstructions from two different perspectives.
2D 키포인트에서 3D 포즈를 추정하는 것은 (i) 깊이 모호성: 그림 1 (a)에 나온 것처럼 다대 1 3D-to-2D 포즈 매핑에 의해 야기됨; (ii) 자가 폐색: 그림 1 (a-e)에 표시된 것처럼 특정 인간 포즈 아래에서 발생함; (iii) 인간의 부정확한 포즈 오류로 인해 여전히 잘못된 포즈 포즈로 남아 있습니다.
깊이 모호성을 완화하기 위해, 일부 작업[4], [5]에서는 생성된 3D 구조의 합리성을 정규화하기 위해 약하게 감독되는 방법을 도입합니다. 예를 들어 Driver 등입니다. [5]는 임의의 2D 대 3D 투 3D 투영을 통해 3D 구조에 선행 조건을 부과하기 위해 적대적 프레임워크를 활용합니다. 그럼에도 불구하고, 자가 폐색 문제는 여전히 추정된 비디오에서 떨리는 움직임뿐만 아니라 해결하기도 어렵습니다. 이러한 문제를 해결하기 위해, 시간적 모델링은 보다 부드러운 움직임을 생성하기 위해 순차적 모델에서 공동 조정 벡터를 사용해 왔습니다 [6], [7]. 그러나, 조인트 시퀀스의 벡터 표현은 공간 관계에 대한 표현성이 부족하며, 이는 깊이 모호성과 자기 혼동을 완화시키는 데 중요합니다. 시공간 정보를 최대한 활용하기 위해 Cai et al. [8]은 공간 구성과 시간적 일관성을 구성하기 위해 로컬-글로벌 네트워크를 설계하며, 이는 시공간 그래프로 2D 키포인트 시퀀스를 취합니다. 그러나 시간 관계를 인코딩하기 위해 그래프 컨볼루션 네트워크를 사용하는 것은 장기 종속성을 효과적으로 모델링할 수 없습니다. 이 네트워크 아키텍처도 입력 고정 길이로 제한됩니다.
2D에서 3D 비디오 기반 방법이 상당히 발전했음에도 불구하고 다음과 같은 중요한 특성을 통합하는 방법은 없습니다.
(i) 2D 키포인트 시퀀스와 자세 의미론의 계층 구조에서 보다 유익한 상황 시공간 정보를 추출하여 깊이 모호성을 해결하고, 자기 혼동을 완화하며, 움직임을 부드럽게 합니다.
(ii) 비디오는 다양한 길이 시퀀스를 효과적으로 보여 주는 유연한 입력 프레임 길이 처리 기능을 제공합니다.
(iii) 중복 중간 프레임 계산 없이 3D 포즈의 실시간 추정입니다. 실시간 추정을 통해 골격 기반 동작 인식과 인간-로봇 상호 작용을 실시간으로 결합하는 등 의미 높은 시각적 작업의 다운스트림 결합을 촉진합니다.
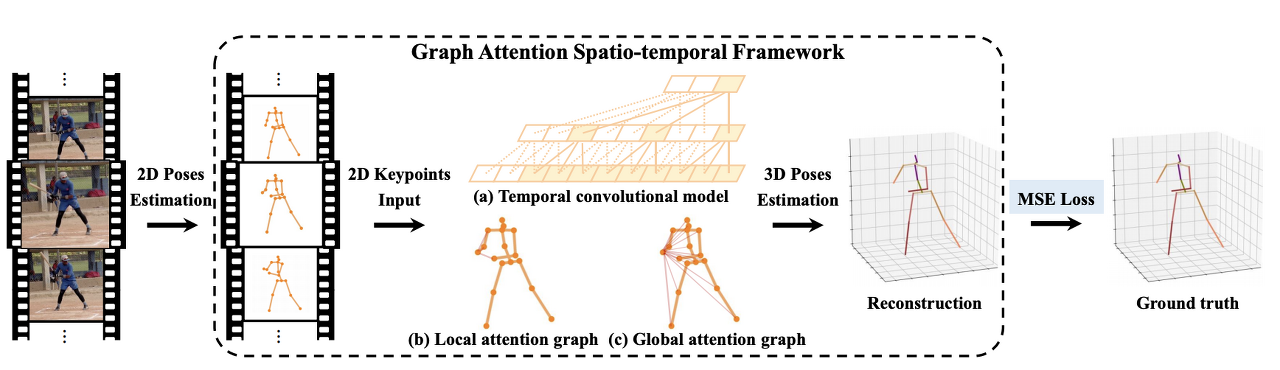
- Fig. 2: Schematic overview of the GAST-Net framework. The input consists of consecutive 2D pose estimates from RGB images. The output is a sequence of reconstructed 3D poses from the corresponding 2D keypoints. GAST-Net synergistically interleaves 3 components: (a) a dilated 팽창된 temporal convolutional model (with 2D keypoint sequences as input (bottom) and 3D pose estimates as output (top)) with (b) a set of local attention mechanisms for visualized joints (i.e. the right-wrist) including local kinematic dependencies and symmetric relations, and (c) a global attention mechanism that informs about posture semantics.
이러한 과제는 우리에게 더 풍부한 시공간 표현을 연구하고 공간 및 시간 정보를 유연하게 인터리빙하도록 영감을 줍니다. 이를 위해, 우리는 그래프 주의 블록을 통해 인간 운동학적 제약의 세 가지 측면을 더 잘 학습하고 확장된 컨볼루션(convolution)을 활용하여 장기적인 시간적 컨텍스트를 모델링하는 인터리빙 그래프 주의 시공간 네트워크를 기여합니다. 그래프 주의 블록은 골격 관절 대칭, 원위 관절에서의 국소 운동학적 관계 및 전역 자세 관절 의미론을 학습합니다. 확장된 시간적 컨볼루션 네트워크(TCN)는 다양한 시퀀스를 유연하게 캡처하고 인과 컨볼루션과 협력하여 실시간 포즈 추정을 달성할 수 있습니다 [7], [9] (그림 2 (a) 참조). 단일 프레임 시나리오의 경우, 확장된 컨볼루션은 새로운 모델을 재교육할 필요 없이 신속하게 추론할 수 있습니다 [7]. 우리의 연구에서, 우리는 공간적이고 시간적인 데이터가 이질적인 것을 이해합니다. 따라서 우리는 그들을 독립적으로 대하지만 TCN의 이점을 활용할 수 있도록 시너지 효과를 발휘하는 방식으로 그들을 중재합니다.
시간 모델링과 관련하여, 우리는 [7]의 확장된 시간 컨볼루션에 기반하지만, 3차원 시공간 시퀀스를 다루기 위해 설계를 확장합니다. 공간 모델링과 관련하여, 로컬 연결 및 대칭의 로컬 공간 특성은 그래프 컨볼루션 네트워크(GCN)를 통해 모델링되며, 시스템에서 "로컬 어텐션 그래프"라고 합니다(그림 2 (b) 참조). 전역 공간 특성의 경우 [10]에서 영감을 끌어내고 그래프 주의 네트워크[11]를 활용하여 데이터 중심 학습으로 자세 의미론을 표현합니다. 이러한 블록을 "전역 주의 그래프"라고 하며 그림 2(c)에 나와 있습니다. 그래프 주의 블록은 인체의 계층적 대칭 구조를 효과적으로 표현하고 시간이 지남에 따라 글로벌 의미 정보를 적응적으로 추출합니다. 특히, 국소 및 전역 공간 블록은 2D 키포인트 시퀀스의 시공간 특징을 효과적으로 추출하고 융합하기 위해 시간 블록과 상호 작용합니다(그림 3 참조).
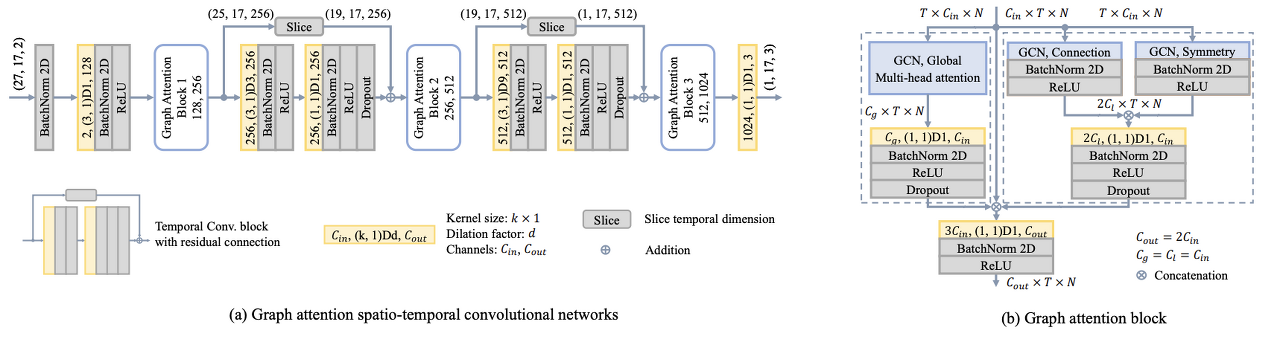
- Fig. 3: (a) An instantiation of GAST-Net for 3D pose estimation. The GAST-Net consists of 2 Temporal Convolution Blocks and 3 Graph Attention Blocks. Given a 2D pose sequence, the output is a sample 1-frame prediction. Dimensions are enclosed in parenthesis: e.g. (27, 17, 2) denotes a receptive field of 27 frames, 17 joints, and 2 channels. (b) The graph attention block architecture. The left dotted box indicates the local graph attention layer. The right dotted box indicates the global graph attention layer. The layer outputs is concatenated followed by a 2D convolution layer before outputting the spatio-temporal features.
II. RELATED WORKS
A. 2D-to-3D Pose Estimation
마르티네즈 [2]는 2D 접합 위치를 3D 위치로 끌어올리는 간단하고 효과적인 선형 레이어를 제안했습니다. 많은 작업[3], [4], [12]은 기본 2D 키 포인트에서 정확한 3D 포즈 추정을 생성하려고 했습니다. 완트 [4]에서는 생성된 3D 포즈를 2D 영상에 다시 투영하고 이를 실제와 비교하여 과적합을 해결하기 위한 준지도 접근법을 제안했습니다. 왕 [12]는 실내 3D 입력이 필요 없이 야생에서 고품질 3D 포즈를 생성할 수 있도록 기하학적 검색 체계를 갖춘 새로운 스테레오 네트워크를 설계했습니다. 그럼에도 불구하고, 하나의 이미지에서 정확한 3D 포즈를 생성하는 것은 잘못된 문제입니다. 최근 연구는 보다 강력하고 부드러운 3D 포즈를 얻기 위해 시간적 정보를 활용했습니다 [3], [6]–[8], [13]. 예를 들면, 호사인[6]에서는 먼저 2D 포즈를 고정 피처 벡터로 인코딩한 다음 3D 포즈로 디코딩하는 잔류 연결을 가진 2계층 정규화된 LSTM 네트워크를 제안했습니다. 그러나 2차원 포즈를 1차원 벡터로 인코딩하면 2D 포즈의 공간 구성 표현은 무시됩니다. 다른 최근의 연구는 공간 구성 제약 조건 및 시간 정보를 통합하여 3D 포즈를 추정합니다 [8], [14]. Wang[14] 등은 U자형 그래프 컨볼루션 네트워크를 설계하여 시간 풀링 작업을 통해 장거리 정보를 수집했습니다. Cai[8] 등에서는 그래프 풀링 및 그래프 업 샘플링이 활용되어 규모에 관계없이 기능을 처리하고 통합합니다. 그러나, 그들의 로컬-글로벌 네트워크 아키텍처는 고정 길이의 시공간 시퀀스를 포함하기에 제한적입니다.
B. Spatio-Temporal Graph
GCN은 그래프 구조화된 데이터에 대한 컨볼루션을 일반화하며 대략 스펙트럼 기반 및 공간 기반 범주로 분류됩니다 [1], [15], [16]. 공간 기반 GCN은 우리의 작업과 더 관련이 있습니다. 우리의 공간 네트워크는 [1]과 [16]이 제안한 GCN을 모두 사용하여 각 조인트의 로컬 및 전역 기능을 얻습니다. 비유럽 데이터에서의 GCN의 뛰어난 성능으로 인해, 골격 기반 동작 인식[10], [17] 및 동작 예측[18]을 포함하여 인간의 작업을 이해하기 위해 골격 시퀀스를 시공간 그래프로 모델링하는 최근의 많은 연구도 있습니다. 우리의 접근 방식은 그래프의 토폴로지를 확장하고 공통 컨볼루션 네트워크를 결합하여 시공간 정보를 통합하는 적응형 그래프 컨볼루션 블록[10]과 약간의 유사성을 가지고 있습니다. 그러나 우리의 연구는 네 가지 뚜렷한 특징을 가지고 있습니다: (i) 중력을 기반으로 국소 공간 구성을 세 개의 하위 집합으로 설정하는 대신, 우리의 접근 방식은 운동학적 관절 제약뿐만 아니라 인체의 대칭적 계층 구조를 모델링하는 것을 목표로 합니다. (ii) 국소 및 전역 인접 행렬은 명시적으로 다른 그래프 컨볼루션에 적용됩니다. 다양한 공간 의미론을 추출합니다. (iii) 확장된 컨볼루션(convolution)은 장기 시간 정보를 효과적으로 모델링하는 데 사용되며, (iv) 개시 모듈과 마찬가지로 3차원 공간 의미 기능을 더 잘 통합하기 위해 연결을 활용한다.
III. APPROACH
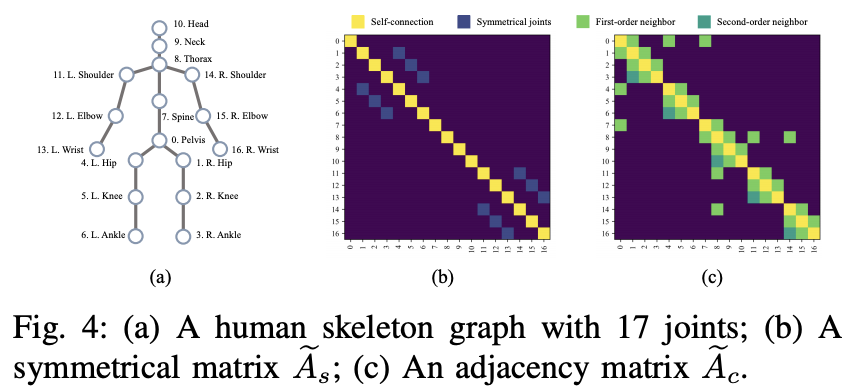
비디오에서 2D 포즈 예측 시퀀스가 주어지면, 우리의 목표는 골반이라는 루트 조인트를 기반으로 3D 좌표 시퀀스를 출력하는 것입니다(그림 4 (a) 참조). 이 섹션에서는 인터리빙 그래프 주의 시공간 네트워크를 소개합니다. 시간적 구성요소는 확장 TCN으로부터 장기적 패턴(Sec. III-A)을 다루기 위해 설계되었습니다.
공간 구성요소에 대해서는
- 인간 골격의 계층적 및 대칭 구조를 모델링하는 로컬 공간 주의 네트워크(Sec. III-B)와
- 인체의 공간 특성을 더 잘 인코딩하기 위해 글로벌 의미 정보를 적응적으로 추출하는 글로벌 공간 주의 네트워크(Sec. III-C)
- 그림 3 (a)는 27 프레임의 수용적 필드 크기로 제안된 프레임워크의 인스턴스화를 묘사하고, 그림 3 (b)는 로컬 및 전역 공간 블록으로 구성된 그래프 주의 블록을 묘사합니다.
A. Temporal Convolutional Network
원래의 시간확장 컨볼루션 모델 [7]은 커널 크기와 컨볼루션의 확장 계수를 설정하여 수용 필드를 유연하게 제어하는 입력 계층, 출력 계층 및 B 시간 컨볼루션 블록으로 구성됩니다. 각 블록은 먼저 커널 크기 k와 확장 계수 = k^B로 1D 컨볼루션 후 커널 크기 1로 컨볼루션합니다. [7]과 비교한 주요 차이점은 입력 2D 포즈 시퀀스를 3차원 벡터(T, N, C)로 나타낸다는 점입니다. 여기서 T는 수용 필드 수, N은 각 프레임의 조인트 수, C는 좌표 치수(x, y)입니다. 시간 단계에 걸쳐 공간 정보를 저장하기 위해, 우리는 원래의 1D 컨볼루션(convolution)을 k×1의 커널 크기에 대한 2D 컨볼루션(convolution)으로 교체합니다. 동시에 각 배치 정규화가 2D로 변경되고 입력 데이터를 정규화하기 위해 처음에 추가됩니다. 드롭아웃은 일반화를 개선하기 위해 블록의 두 번째 컨볼루션 계층에서만 사용됩니다. 그림 3은 B = 2 블록으로 27 프레임의 수용적 필드 크기에 대한 GAST-Net의 인스턴스화를 보여줍니다. TCN의 네트워크 특성에 따라, 제안된 모델은 필요에 따라 다양한 수의 긴 시퀀스 수용 필드를 훈련할 수 있습니다.
B. Local Attention Graph
주어진 프레임에서 2D 키포인트는 인간 골격의 관절을 나타냅니다. 골격은 자연스럽게 관절을 노드로, 인간 링크를 에지로 하는 무방향 그래프로 표현됩니다. 우리는 Zhao[1]가 제안한 SemGCN을 기반으로 주어진 프레임에 대한 2D 키포인트의 골격 그래프를 구성합니다. 우리는 골격 2D 포즈를 그래프 G = (V, E)로 정의하며, 여기서 V는 N개의 노드와 E 에지의 집합입니다. X = {x1, x2, . . , xN | xi r R 1×C }은 C 채널이 있는 노드 기능 집합입니다. 그래프의 구조는 관절과 자기 연결을 나타내는 아이덴티티 매트릭스 I 사이의 기존 연결을 나타내는 1차 인접 행렬 A β R N×N에 의해 초기화될 수 있습니다. Ae = (A + I)는 GCN으로 컨볼루션 커널을 나타냅니다. SemGCN의 정의에 따르면, l-th 레이어의 노드 특징을 고려할 때, 후속 레이어의 출력 특징은 다음과 같은 컨볼루션으로 얻어집니다.
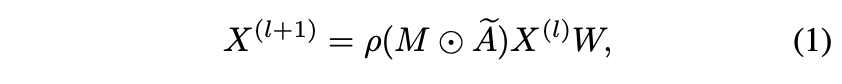
여기서 W ∈ R Cl×Cl+1은 출력 채널을 변환하는 데 사용되는 학습 가능한 매트릭스입니다, M ∈ R N×N은 학습 가능한 마스크 매트릭스이며, 요소별 곱셈 연산이며, is는 다음과 같습니다. 그래프의 해당 인접 노드에 대한 노드 기능의 기여를 정규화하는 소프트맥스 비선형성입니다.
출력 노드 기능의 채널에 대해 일련의 마스크 매트릭스 Mc ∈ R N×N을 도입함으로써 Eqtn.1을 다음으로 확장할 수 있습니다.
여기서 k는 채널별 연결을 나타내며 wc는 행렬 W의 c-행입니다.
Eqtn.2는 인접 노드 간에 고유한 의미론을 공동으로 학습합니다. 그러나 매우 주목할 만한 1차 이웃 표현은 (i) 몸통 중심 인체의 대칭 구조와 (ii) 인체의 운동학적 제약 조건을 제대로 모델링하지 못합니다. 따라서, 우리는 인체에서 대칭적인 기능과 관련된 구조적 지식을 명시적으로 고려할 것을 제안합니다. 게다가, 1차 이웃 표현이 인간의 공간 관계를 모델링하기 위해 애쓰는 또 다른 이유는 공동 제약 조건이 1차 이웃 관절에 국한되기 때문입니다. 더 정확히 말하면, 운동 사슬의 끝에 위치한 손목, 발목, 그리고 머리와 같은 원위 관절은 단지 하나의 1차 이웃 관절만을 가지고 있습니다. 따라서, 그들의 우주에서의 위치는 1차 이웃 때문에 효과적으로 위치해 있지 않습니다. 이러한 조인트는 모델링 오류의 가장 큰 단일 소스입니다 [6]. 그럼에도 불구하고, 우리는 위치 모호성을 완화하기 위해 하사지(발찌-무릎), 상사지(팔꿈치-어깨), 축체(머리-목-흉부)의 하위 세그먼트에 걸친 관계를 이용합니다.
앞에서 언급한 제한에 기초하여, 우리는 (i) 대칭적인 상대(즉, 사지 관절)를 가진 관절에 대한 인간 골격 대칭 구조를 인코딩하는 대칭 행렬 Aes(그림 4 (b) 참조)라는 두 가지 새로운 컨볼루션 커널을 설계합니다. (ii) 원위 관절(즉, 발목-무릎, 발목-엉덩이)에 대한 1차 및 2차 (키네마틱) 연결을 명시적으로 인코딩하는 인접 행렬 Aec(그림 4 (c) 참조) 나머지 노드는 1차 연결을 통해서만 모델링됩니다.
이 두 컨볼루션 커널은 각각 두 개의 개별 GCN에 적용되며, 여기서 각 GCN은 그림 3 (b)의 오른쪽 점박스에 표시된 대로 배치 정규화 및 정류 선형 단위에 이어집니다.
C. Global Attention Graph
골격의 하위 부분(예: 손목-발목)에 걸쳐 존재하는 분리된 관절 간의 관계는 글로벌 자세 및 제약 정보(생각 실행)를 인코딩하는 데 핵심적인 역할을 합니다. 이와 같이, 분리된 공동 표현은 깊이 모호성과 혼돈을 해결하는 데 도움이 됩니다. 비국소 관계를 적응적이고 효과적으로 인코딩하기 위해, 우리는 Eqtn.2에 도입된 메커니즘을 1차 관계에서 글로벌 관계로 확장하는 다중 헤드 주의 메커니즘을 가진 글로벌 종단 간 GCN을 제안한다. 글로벌 어텐션 메커니즘은 Eqtn. 3에 먼저 소개된 후 자세히 설명합니다.
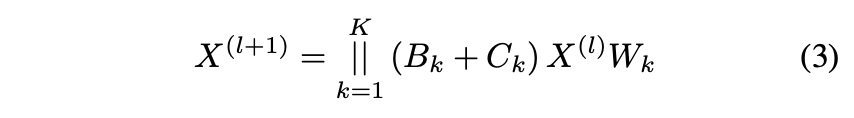
여기서, K는 주의 헤드의 수이고, Bk r R N×N은 적응형 글로벌 인접 매트릭스, Ck n R N×N은 학습 가능한 글로벌 인접 매트릭스, W × R Cl×(Cl/K) 는 변환된 행렬입니다. 본 연구에서는 K = 4개의 병렬 주의 헤드를 설정합니다. 다음으로, 우리는 재정의된 인접 행렬 Bk와 전역 인접 행렬 Ck에 대해 자세히 논의합니다.
Bk는 각 노드의 고유한 그래프를 학습하는 데이터 종속 행렬을 나타냅니다. [16]에서 제안한 주의 계수 함수를 채택하여 노드 간 연결이 존재하는지 여부와 연결 강도가 어느 정도인지 판단합니다. 즉, xi와 xj의 두 노드 기능이 주어지면 먼저 두 개의 임베딩 함수인 β와 β를 적용하여 Cl에서 Cl/K 채널까지 각 노드의 기능을 다운샘플링합니다. 각 노드의 채널 수가 감소하므로 다중 주의에 대한 총 계산 비용은 전체 채널이 있는 단일 헤드 주의의 총 계산 비용과 유사합니다. 그런 다음 두 개의 내장된 기능을 연결하고 가중치 벡터 wf로 도트 제품을 계산하여 스칼라 출력을 생성합니다. 노드 간 계수 비교를 용이하게 하기 위해 softmax 함수에 의해 스칼라 출력이 정규화됩니다. 작업은 Eqtn에 나와 있습니다. 4:
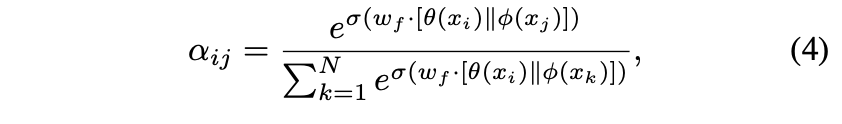




댓글